Useful formulas related to parallelograms along with brief descriptions. These formulas could be applied for solving math and geometry problems involving parallelograms and related shapes. The examples illustrate how the formulas for parallelograms can be applied in various real-life situations, from construction and design to engineering and geometry.
- Solve: Parallelogram practice problems, exercises, tests;
- Answer: Parallelogram Quiz and trivia Questions;
Parallelogram Formulas
Area of a Parallelogram (A):
- Formula 1: A = base × height
- Formula 2: A = a × b × sin(angle)
- Formula 3: A = e × f × sin(angle)
- Description: Calculate the area of parallelograms based on the given information and solve geometric problems across various contexts:
Formula 1: The most common method is to multiply the length of the base by the perpendicular height (or altitude) to that base. This is given by A = base × height and represents the amount of space enclosed by the parallelogram.
Formula 2: If you have the lengths of two adjacent sides (a and b) and the included angle (angle) between them, you can use the formula A = a × b × sin(angle) to find the area. This trigonometric approach is especially useful when the perpendicular height is not directly available.
Formula 3: Another way to calculate the area when you have two non-parallel sides (e and f) and the included angle (angle) is to use the formula A = e × f × sin(angle). This formula is particularly handy when you have a slanting parallelogram.
The angle should be measured in radians when using the trigonometric formulas.
Perimeter of a Parallelogram (P):
- Formula: P = 2 × (length of base + length of adjacent side);
- Or Formula 2: a + b + c + d (when a, b, c, d are representing 4 sides of a parallelogram) to: 2 (a+b).
- Description: The perimeter of a parallelogram is the total length of its four sides. It can be found by adding twice the sum of the length of the base and the length of an adjacent side.
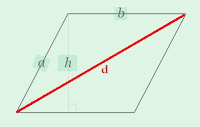
Diagonal Lengths of a Parallelogram (d1 and d2) - If the two diagonals are equal, you have a rectangle and the length of the diagonal can be obtained using the Pythagorean theorem:
- Formula for d1: d1 = √(base^2 + height^2)
- Formula for d2: d2 = √(base^2 + height^2)
- Description: A parallelogram has two diagonals, and each diagonal connects opposite vertices. The lengths of these diagonals can be found using the Pythagorean theorem, where the base and height of the parallelogram form the two sides of a right triangle.
Interior Angles of a Parallelogram (θ1 and θ2):
- Formula: θ1 = θ2 = 180° - α
- Description: In a parallelogram, opposite angles (α) are congruent, which means they have the same measure. So, to find the measures of the interior angles θ1 and θ2, you can subtract the measure of one of the opposite angles from 180°.
- Formula: θ1 = θ2 = 180° - α
Height of a Parallelogram (h):
- Formula: h = A / b;
- Description: "h" is the height of the parallelogram. "A" represents the area of the parallelogram. "b" denotes the length of one of the parallel sides (the base). This formula expresses that the height of a parallelogram is equal to the ratio of its area to the length of its base.
Length of a Diagonal in a Parallelogram (x) - using the Law of Cosines :
- Formula: x = √(a^2 + b^2 - 2ab * cos(A)) = √(a^2 + b^2 - 2ab * cos(B));
- Description: In this formula: "x" represents the length of the diagonal. "a" and "b" are the lengths of the two adjacent sides. "A" and "B" are the angles between the diagonal and each of the adjacent sides. This formula allows you to find the length of a diagonal in a parallelogram when you know the lengths of the adjacent sides and the included angle(s).
Area of a Parallelogram Using Vectors:
- Formula: A = |a × b|
- Description: In vector mathematics, the area of a parallelogram with sides defined by vectors 'a' and 'b' can be calculated by taking the magnitude (absolute value) of their cross product, denoted as |a × b|.
Formula of parallelogram sides in terms of diagonals and the angle between the diagonals:
- a = √(d1^2 + d2^2 - 2d1d2cos(γ))
- b = √(d1^2 + d2^2 + 2d1d2cos(γ))
- Description: These formulas calculate the sides of a parallelogram (a and b) based on the lengths of its diagonals (d1 and d2) and the angle (γ) between them. The angle can also be represented as δ.
Formula of parallelogram sides in terms of diagonals and another side:
- a = √(2d1^2 + 2d2^2 - 4b^2) / 2
- b = √(2d1^2 + 2d2^2 - 4a^2) / 2
- Description: These formulas find the sides of a parallelogram (a and b) when you know the diagonals (d1 and d2) and one of the sides (b or a).
Formula of parallelogram sides in terms of altitude (height) and sine of an angle:
- a = h / sin(α)
- b = h / sin(α)
- Description: These formulas determine the sides of a parallelogram (a and b) using the height (h) and the sine of one of the angles (α).
Formula of parallelogram sides in terms of area and altitude (height):
- a = A / ha
- b = A / hb
- Description: These formulas compute the sides of a parallelogram (a and b) when you have its area (A) and the corresponding altitude (ha or hb).
Formula of parallelogram sides in terms of Perimeter:
- a = (P / 2) - b
- Description: These formulas find the sides of a parallelogram (a and b) when you know its perimeter (P) and one of the sides (b or a).
Parallelogram Calculation Examples
Example calculations for parallelograms:
Area of a Parallelogram (A):
- Example: If the base of a parallelogram is 6 inches and the height is 4 inches, then the area is A = 6 inches × 4 inches = 24 square inches.
Perimeter of a Parallelogram (P):
- Example: If the base is 5 inches and one of the adjacent sides is 7 inches, then the perimeter is P = 2 × (5 inches + 7 inches) = 2 × 12 inches = 24 inches.
Diagonal Lengths of a Parallelogram (d1 and d2):
- Example: If the base is 8 inches and the height is 6 inches, then both diagonals have the same length: d1 = d2 = √(8 inches^2 + 6 inches^2) = √(64 square inches + 36 square inches) = √(100 square inches) = 10 inches.
Interior Angles of a Parallelogram (θ1 and θ2):
- Example: If one of the opposite angles α is 45°, then θ1 = θ2 = 180° - 45° = 135°.
Height of a Parallelogram (h):
- Example: If the area of the parallelogram is 30 square inches and the length of the base is 5 inches, then the height is h = 30 square inches / 5 inches = 6 inches.
Length of a Diagonal in a Parallelogram (x) - using the Law of Cosines:
- Example: If one side "a" is 7 inches, the other side "b" is 9 inches, and the included angle "A" is 60°, then the length of the diagonal is x = √(7 inches^2 + 9 inches^2 - 2 * 7 inches * 9 inches * cos(60°)) = √(49 square inches + 81 square inches - 126 square inches * 0.5) = √(130 square inches - 63 square inches) = √67 inches.
Area of a Parallelogram Using Vectors:
- Example: Given two vectors a = (3 inches, 4 inches) and b = (2 inches, -1 inch), the area of the parallelogram formed by these vectors is A = |(3 inches, 4 inches) × (2 inches, -1 inch)| = |(3 inches * (-1 inch) - 4 inches * 2 inches)| = |(-3 square inches - 8 square inches)| = 11 square inches.
Examples for Parallelogram side formulas:
Example 1: Using the Formula of Parallelogram Sides in Terms of Diagonals and the Angle Between Diagonals.
Given:
- Diagonal 1 (d1) = 8 inches
- Diagonal 2 (d2) = 6 inches
- Angle between diagonals (γ) = 60 degrees
Using Formula 1: a = √(d1^2 + d2^2 - 2d1d2cos(γ)) a = √(8^2 + 6^2 - 2 * 8 * 6 * cos(60°)) a ≈ √(64 + 36 - 96 * 0.5) a ≈ √(64 + 36 - 48) a ≈ √(52) a ≈ 7.21 inches
Using Formula 1: b = √(d1^2 + d2^2 + 2d1d2cos(γ)) b = √(8^2 + 6^2 + 2 * 8 * 6 * cos(60°)) b ≈ √(64 + 36 + 96 * 0.5) b ≈ √(64 + 36 + 48) b ≈ √(148) b ≈ 12.17 inches
Example 2: Using the Formula of Parallelogram Sides in Terms of Diagonals and Another Side.
Given:
- Diagonal 1 (d1) = 10 inches
- Diagonal 2 (d2) = 6 inches
- Side b = 4 inches
Using Formula 2: a = √(2d1^2 + 2d2^2 - 4b^2) / 2 a = √(2 * 10^2 + 2 * 6^2 - 4 * 4^2) / 2 a = √(200 + 72 - 64) / 2 a = √(208 - 64) / 2 a ≈ √(144) / 2 a ≈ 6 inches
Example 3: Using the Formula of Parallelogram Sides in Terms of Altitude (Height) and Sine of an Angle.
Given:
- Height (h) = 5 inches
- Angle α = 30 degrees
Using Formula 3: a = h / sin(α) a = 5 / sin(30°) a = 5 / 0.5 a = 10 inches
Using Formula 3 (same for side b): b = h / sin(α) b = 5 / sin(30°) b = 5 / 0.5 b = 10 inches
Example 4: Using the Formula of Parallelogram Sides in Terms of Area and Altitude (Height).
Given:
- Area (A) = 60 square inches
- Altitude (ha) = 6 inches (for side a)
- Altitude (hb) = 8 inches (for side b)
Using Formula 4: a = A / ha a = 60 / 6 a = 10 inches
Using Formula 4 (for side b): b = A / hb b = 60 / 8 b = 7.5 inches
Example 5: Using the Formula of Parallelogram Sides in Terms of Perimeter.
Given:
- Perimeter (P) = 28 inches
- Side b = 10 inches
Using Formula 5: a = (P / 2) - b a = (28 / 2) - 10 a = 14 - 10 a = 4 inches
In this example, we use the formula to calculate side 'a' when we know the perimeter (P) and one of the sides (b) of the parallelogram.
Parallelogram Real-life Examples
Real-life calculation examples using the formulas for parallelograms:
Area of a Room Floor:
- Suppose you are an interior designer, and you need to calculate the area of a rectangular room floor to estimate how much flooring material you'll need. If the length of the room is 15 feet, and the width (base of the parallelogram) is 10 feet, you can calculate the floor area using the formula: A = base × height. In this case, A = 10 feet × 15 feet = 150 square feet.
Perimeter of a Fence:
- Imagine you are a landscaper planning to install a fence around a parallelogram-shaped garden. If one side of the garden is 20 yards long (the base), and the adjacent side is 15 yards long, you can find the perimeter using the formula P = 2 × (length of base + length of adjacent side). In this case, P = 2 × (20 yards + 15 yards) = 70 yards.
Cable Length for a Suspension Bridge:
- Engineers designing a suspension bridge need to calculate the length of cables required to support the bridge. If the bridge's base is 300 meters and the height (distance from the base to the center of the bridge) is 80 meters, they can find the length of each diagonal cable using the Pythagorean theorem: d1 = d2 = √(base^2 + height^2). In this case, d1 = d2 = √(300 meters^2 + 80 meters^2) ≈ 316.4 meters.
Angles in a Parallelogram Roof Truss:
- Roof trusses in buildings often have parallelogram shapes. Architects may need to calculate the interior angles of the truss to ensure proper construction. If one of the opposite angles in the truss is 75 degrees, you can find the other interior angles using θ1 = θ2 = 180° - α. In this case, θ1 = θ2 = 180° - 75° = 105°.
Height of a Billboard:
- Advertisers placing a rectangular billboard on an inclined hill need to determine the height of the billboard to ensure visibility from a certain distance. If the area of the billboard is 200 square feet, and the length of the base (width of the billboard) is 10 feet, you can find the height using h = A / b. In this case, h = 200 square feet / 10 feet = 20 feet.
Length of a Support Cable for a Ski Lift:
- Engineers designing a ski lift may need to calculate the length of a diagonal support cable. If one side of the support structure is 50 meters, the other side is 30 meters, and the included angle is 45 degrees, they can use the Law of Cosines: x = √(a^2 + b^2 - 2ab * cos(A)). In this case, x = √(50 meters^2 + 30 meters^2 - 2 * 50 meters * 30 meters * cos(45°)) ≈ 53.66 meters.